Matematyka (Teoria, klasa 7)
Działania na pierwiastkach
Pierwiastki
Kwadrat i sześcian liczby
Dzielenie potęg
Mnożenie potęg
Dodawanie i odejmowanie potęg
Działania na potęgach
Potęgi
Średnia ważona
Średnia arytmetyczna
Ostrosłupy
Równania z jedną niewiadomą
Redukcja wyrazów podobnych
Wyrażenia algebraiczne
Prędkość, droga, czas
Zamiana liczby mieszanej na ułamek niewłaściwy
Zasady obliczania jakim procentem jednej liczby jest druga
Jak obliczyć liczbę, gdy znamy jej procent?
Obliczanie procentu z liczby
Zasady zamiany ułamków na procenty
Najważniejsze informacje o procentach
Skala i mapa
Objętość graniastosłupa prostego
Objętość prostopadłościanu i sześcianu
Objętość
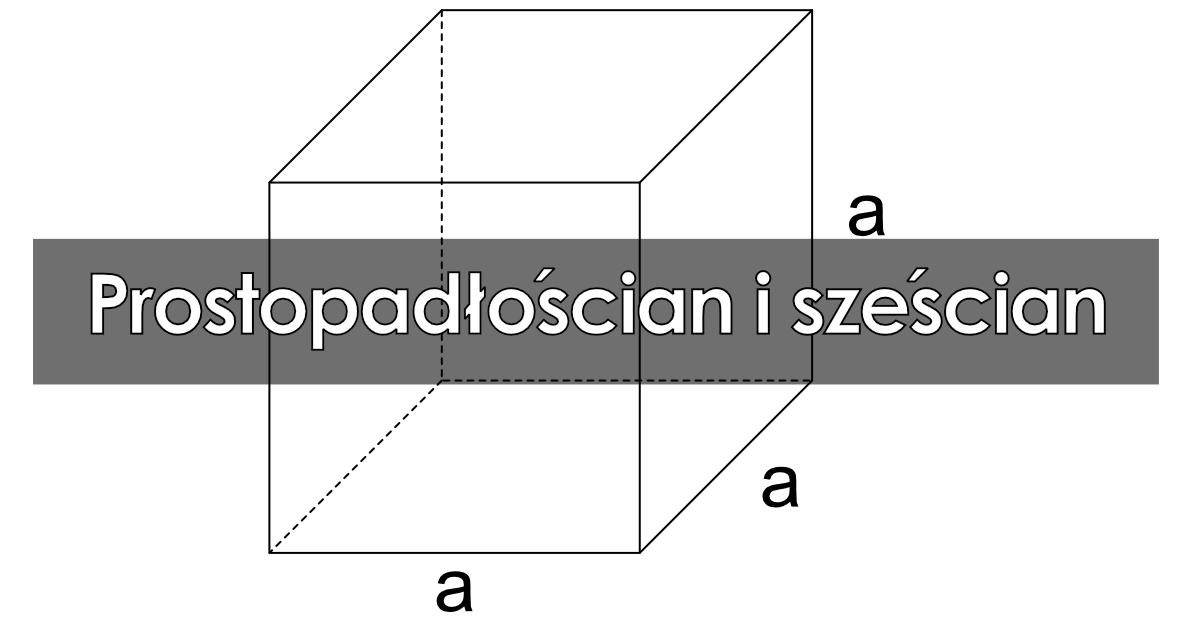
Prostopadłościan i sześcian
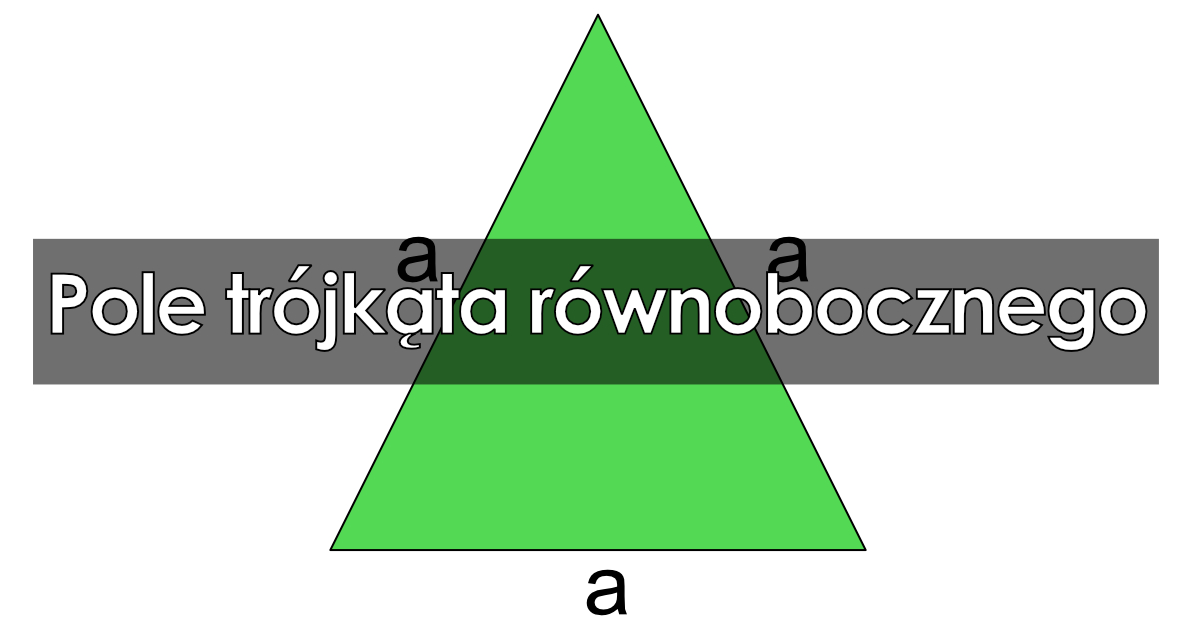
Pole trójkąta równobocznego
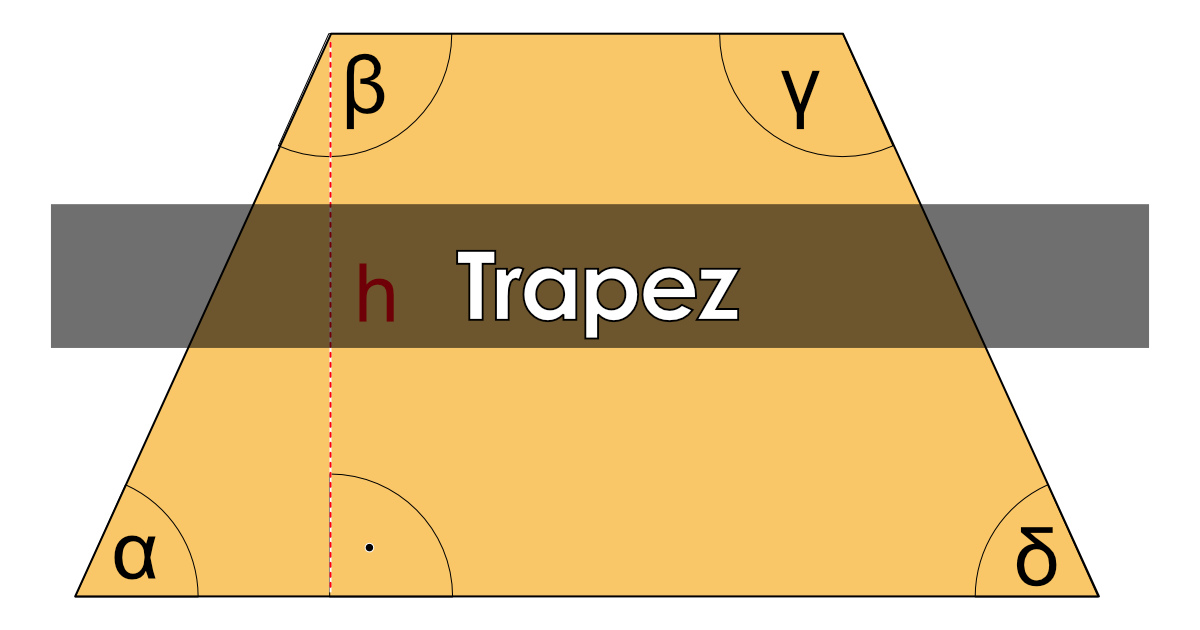
Pole trapezu
Pole równoległoboku i rombu
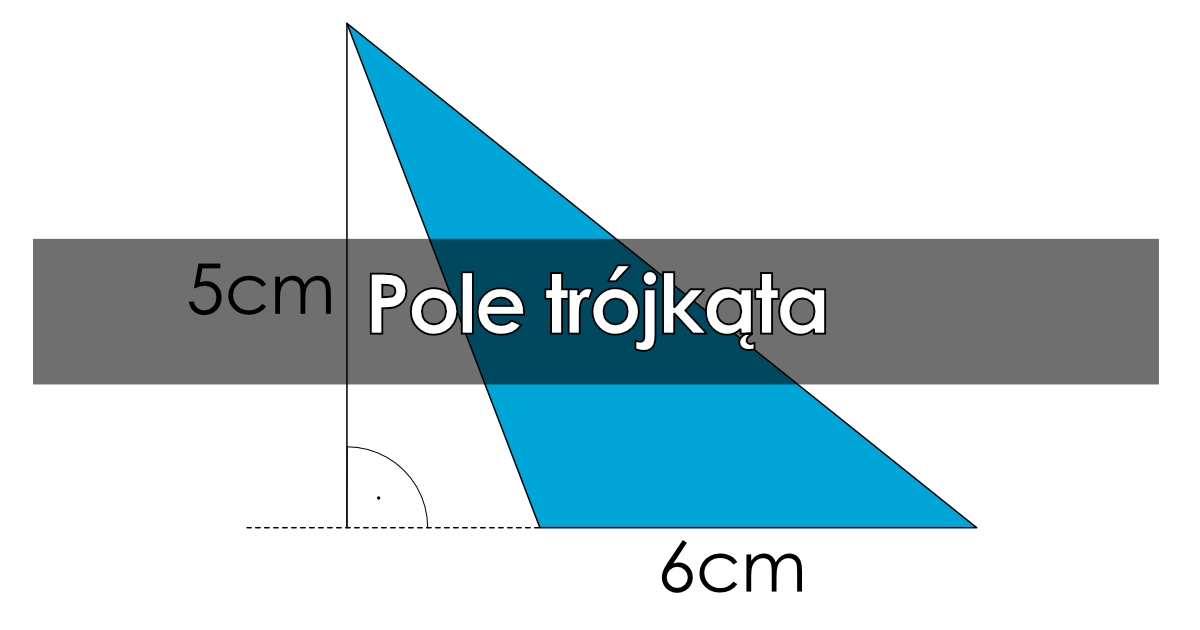
Pole trójkąta
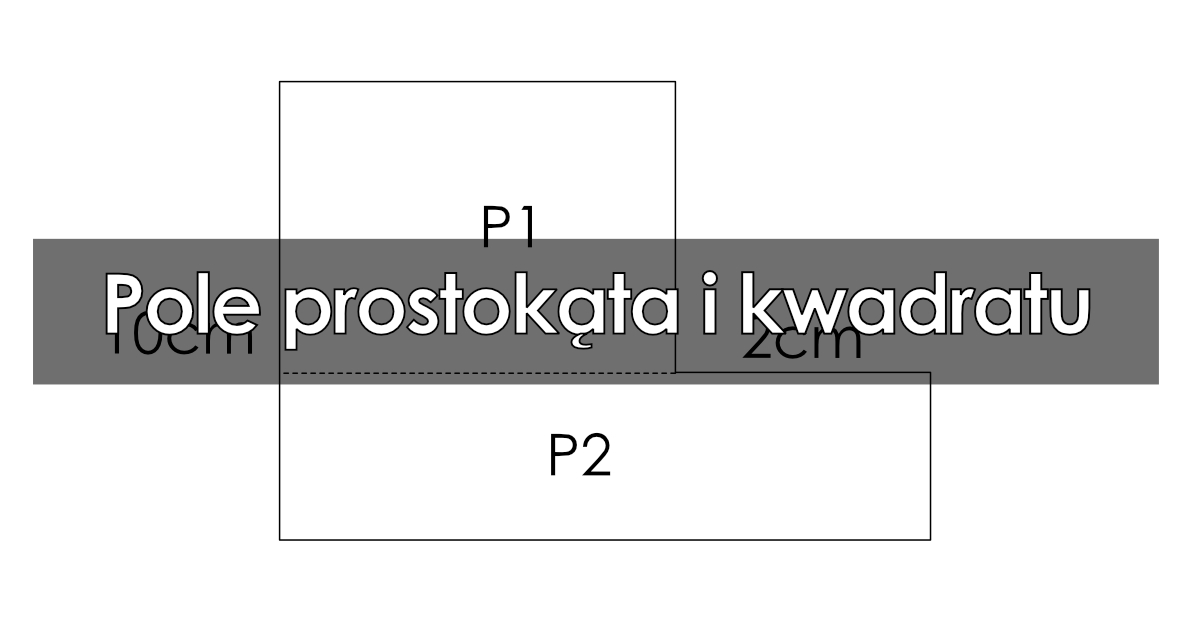
Pole prostokąta i kwadratu
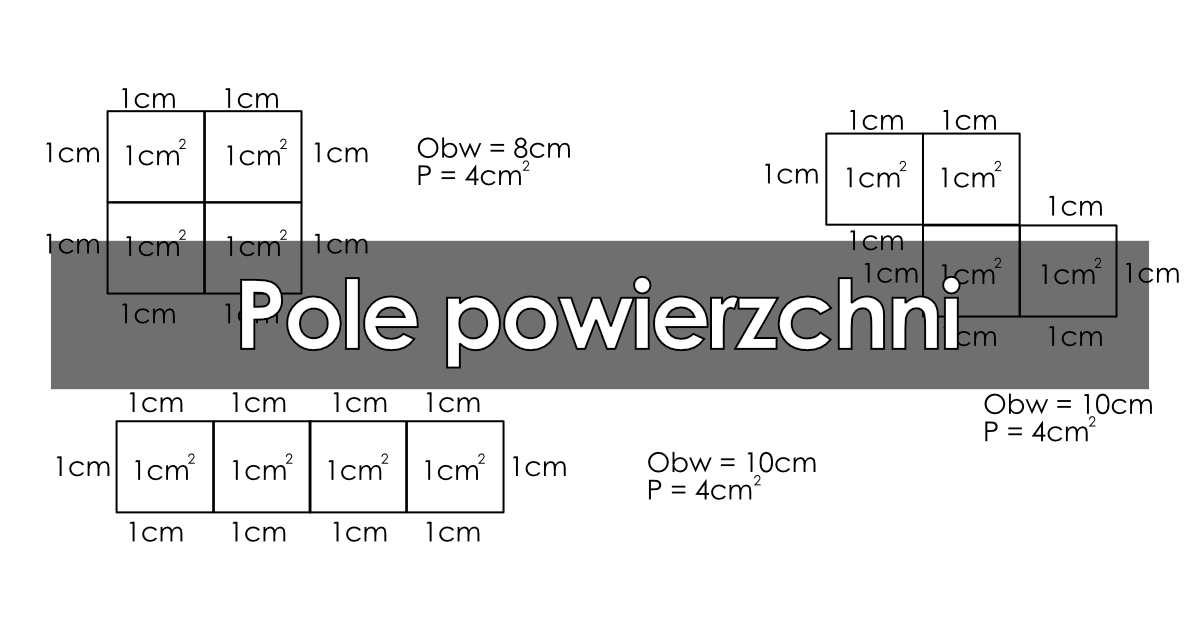
Jednostki pola powierzchni
Pole powierzchni
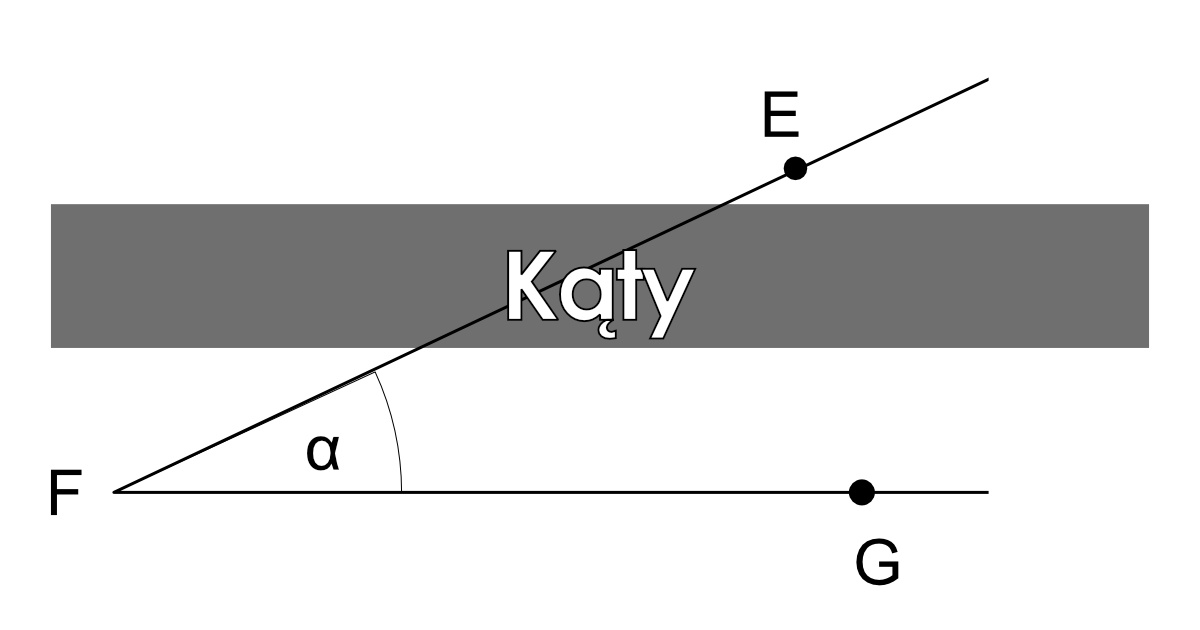
Kąty w trójkącie i czworokącie
Kąty
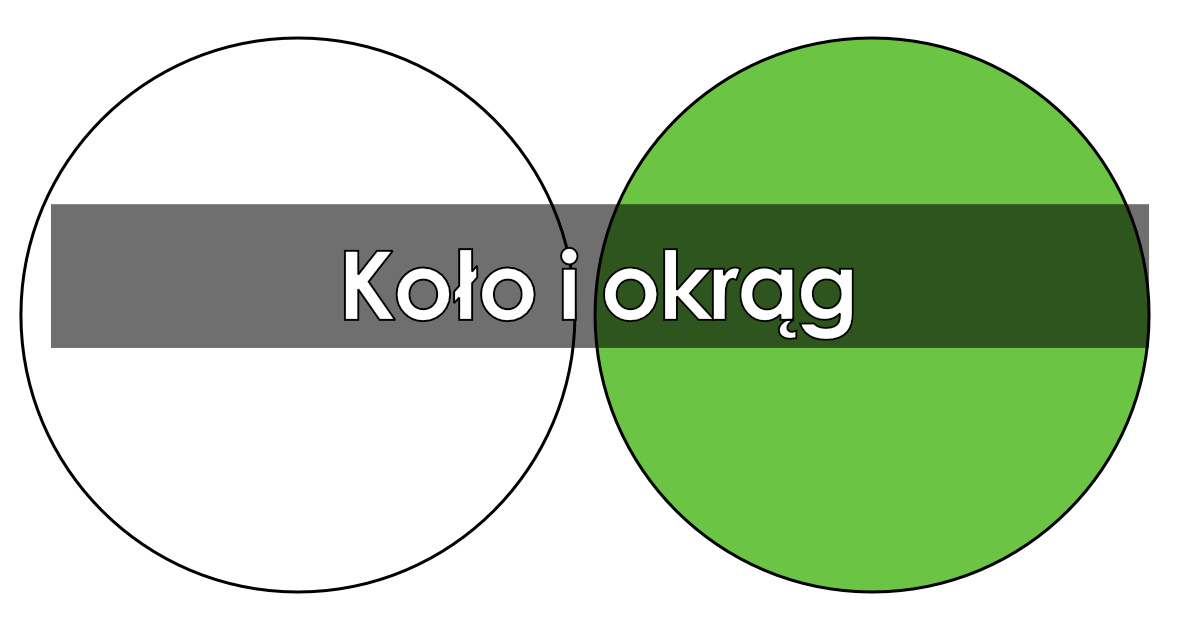
Koło i okrąg
Deltoid
Trapez prostokątny
Trapez równoramienny
Trapez
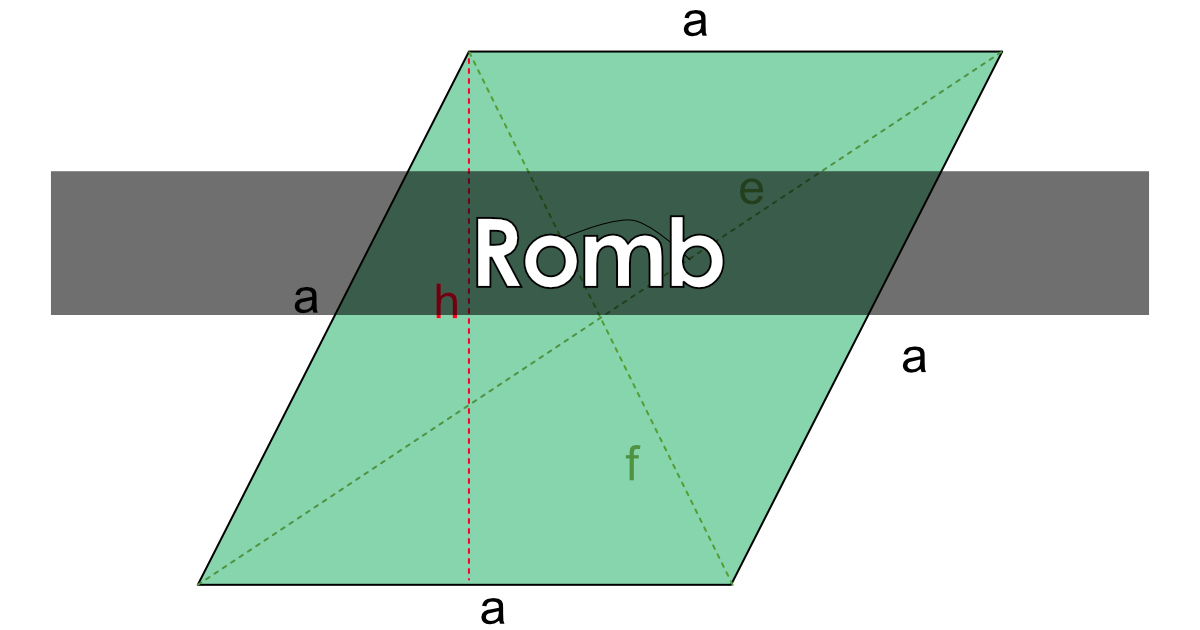
Romb
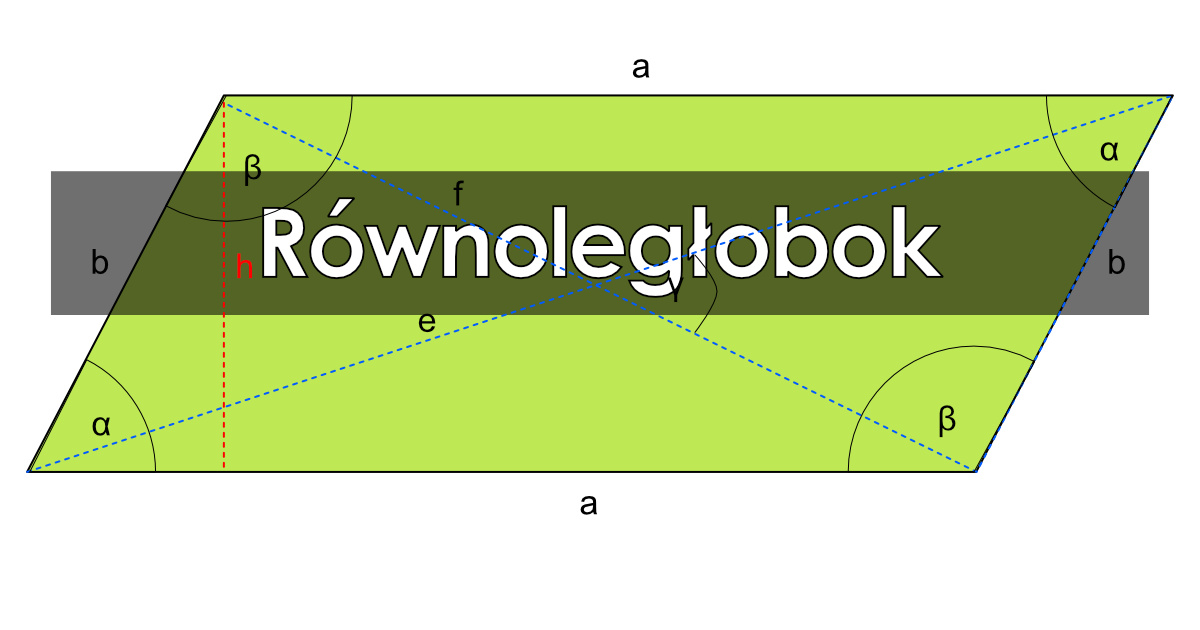
Równoległobok
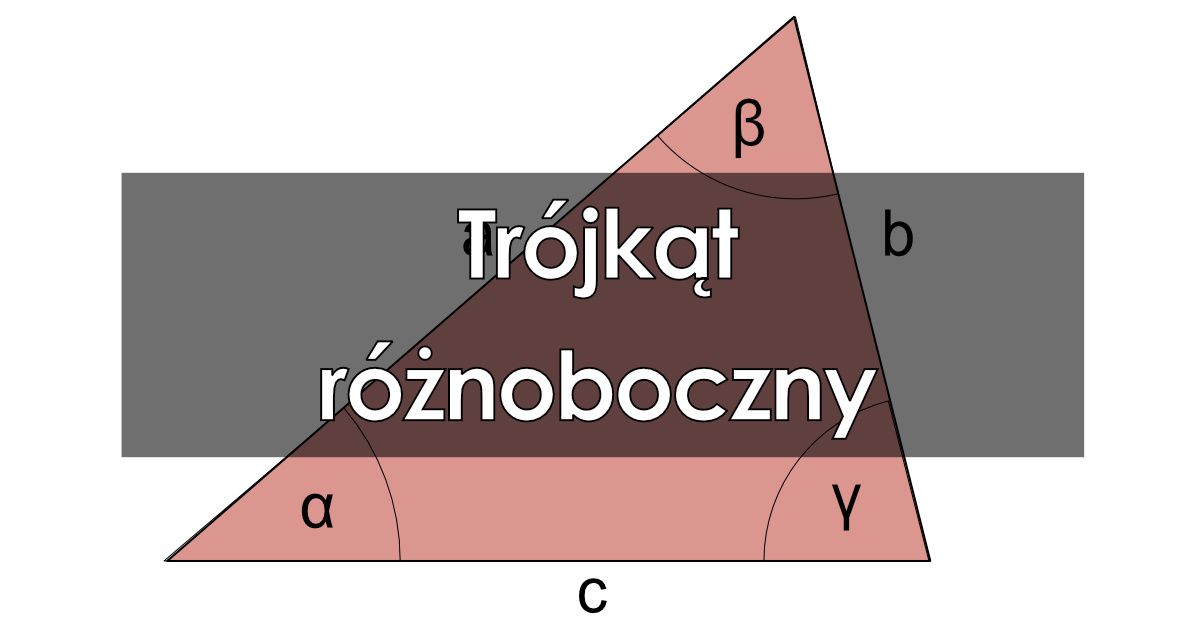
Trójkąt różnoboczny
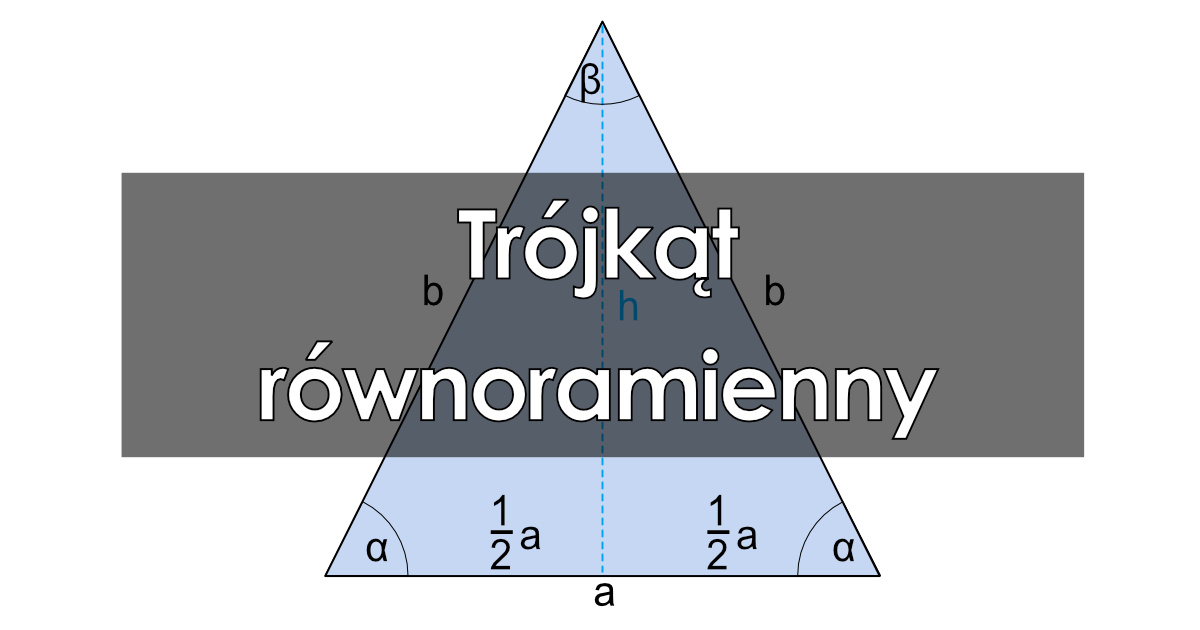
Trójkąt równoramienny
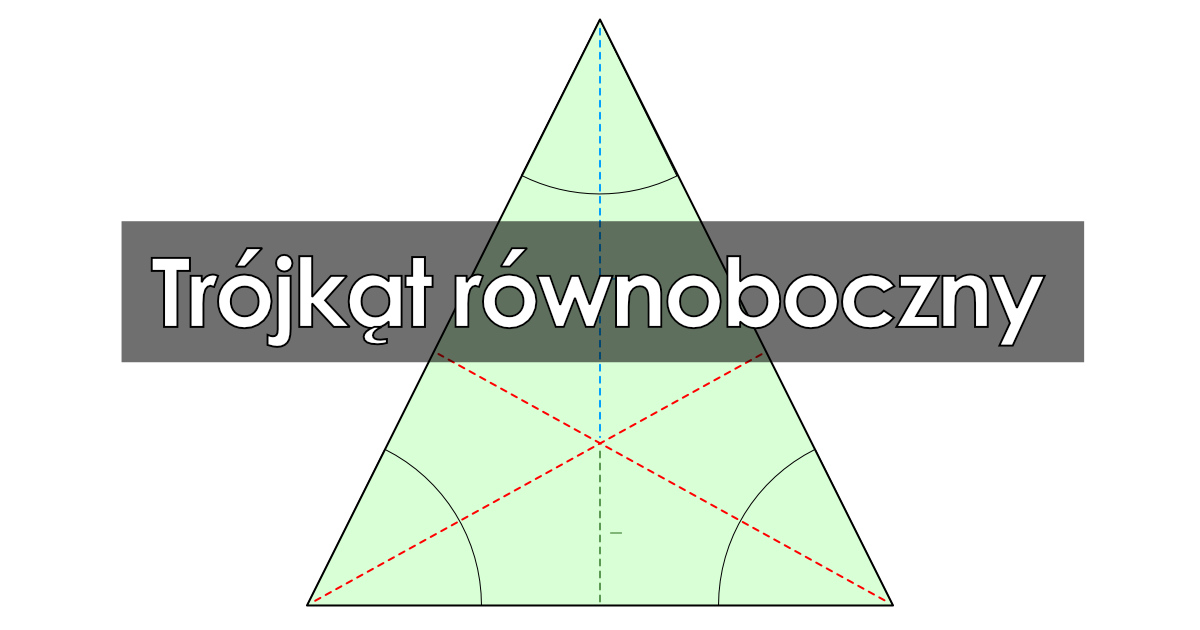
Trójkąt równoboczny
Trójkąt rozwartokątny
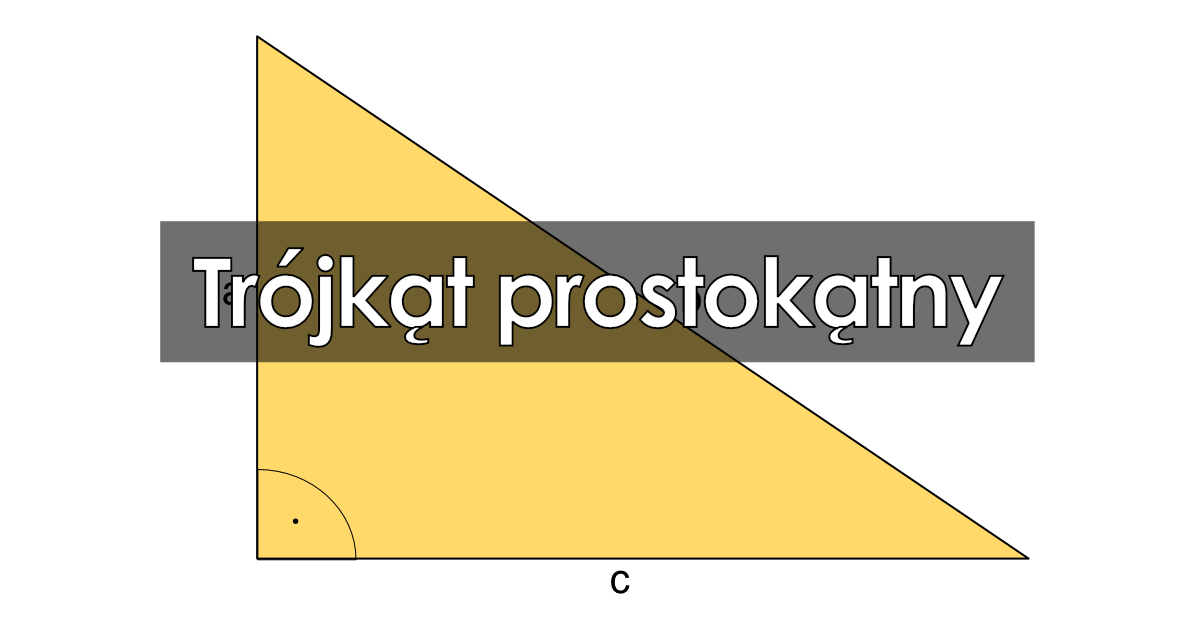
Trójkąt prostokątny
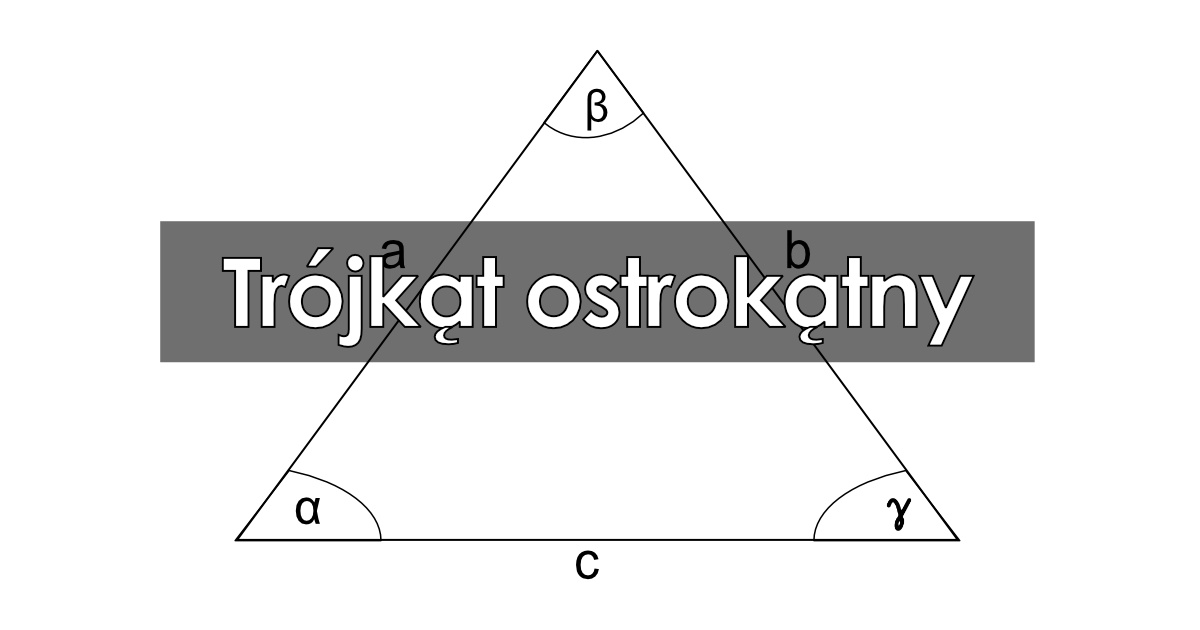
Trójkąt ostrokątny
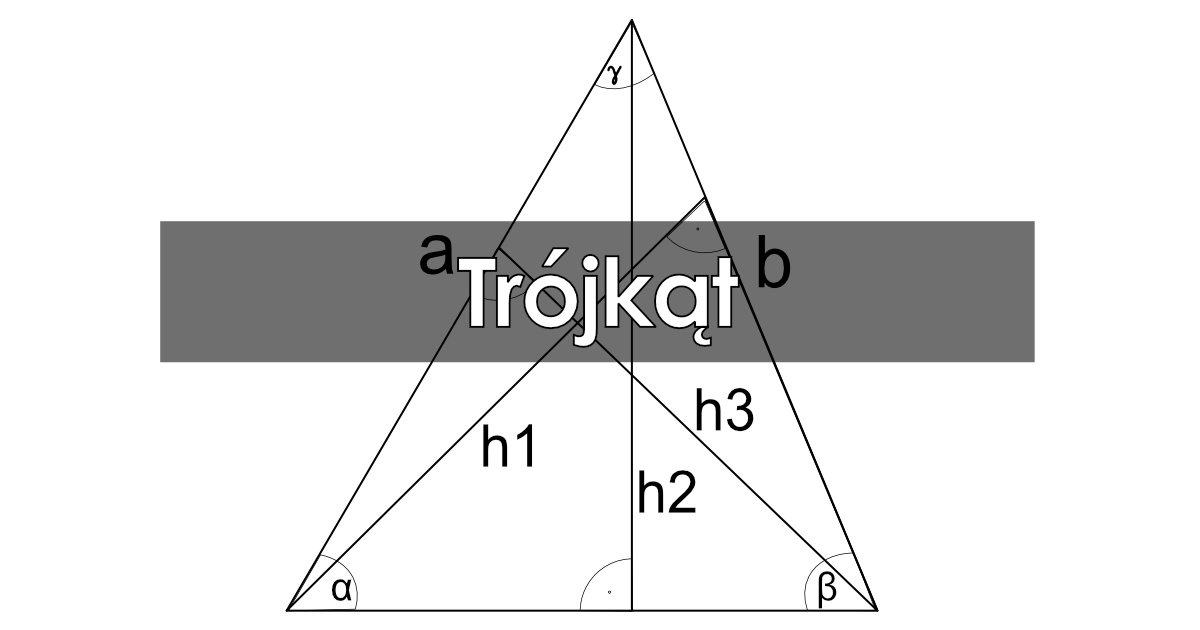
Trójkąt
Prostokąt i kwadrat
Mnożenie i dzielenie liczb ujemnych
Dodawanie i odejmowanie liczb ujemnych
Liczby ujemne – podstawowe informacje
Dzielenie ułamków dziesiętnych
Mnożenie ułamków dziesiętnych
Odejmowanie ułamków dziesiętnych
Dodawanie ułamków dziesiętnych
Mnożenie ułamków zwykłych
Dodawanie i odejmowanie ułamków zwykłych o różnych mianownikach
Sprowadzanie ułamków do wspólnego mianownika
Korzyści płynące z nauki teorii matematyki w klasie 7 jako przygotowanie do kartkówek i sprawdzianów
Nauka teorii matematyki jest kluczowym elementem edukacji dla uczniów klasy 7. Podczas gdy praktyka rozwiązywania zadań jest ważna, zrozumienie teorii daje solidne podstawy, które mogą ułatwić zdobywanie wyższych ocen na kartkówkach i sprawdzianach. Oto kilka korzyści płynących z nauki teorii matematyki.
Rozwija umiejętności rozumienia i interpretacji problemów
Głębokie zrozumienie teorii matematyki pomaga uczniom w interpretacji problemów i zadaniach, które napotkają na kartkówkach i sprawdzianach. Jest to szczególnie ważne, gdy problemy są sformułowane w sposób niekonwencjonalny lub wymagają zastosowania kilku różnych koncepcji matematycznych. Bez solidnej podstawy teoretycznej, tacy uczniowie mogą mieć trudności z zrozumieniem, co dokładnie jest pytane w zadaniu.
Ułatwia rozwiązywanie problemów
Zrozumienie teorii matematyki może również ułatwić proces rozwiązywania problemów. Wiedząc, jakie są podstawowe zasady i prawa matematyki, uczniowie mogą łatwiej zidentyfikować odpowiednie strategie i metody do rozwiązania problemów. Na przykład, zrozumienie teorii liczby pierwszej może pomóc w szybkim rozkładaniu liczb na czynniki pierwsze.
Umożliwia zrozumienie powiązań między różnymi dziedzinami matematyki
Nauka teorii matematyki może pomóc uczniom zrozumieć, jak różne dziedziny matematyki są ze sobą powiązane. Na przykład, teoria liczb, algebra i geometria często łączą się w różnych typach problemów. Zrozumienie tych powiązań może pomóc uczniom zrozumieć, jakie strategie i techniki mogą być najbardziej efektywne w danym kontekście.
Buduje pewność siebie
Ostatecznie, nauka teorii matematyki może pomóc uczniom budować pewność siebie. Wiedząc, że mają solidne podstawy teoretyczne, mogą czuć się pewniej podczas podejmowania prób rozwiązania trudnych problemów na kartkówkach i sprawdzianach. Ta pewność siebie może przekładać się na lepsze wyniki.
W sumie, nauka teorii matematyki oferuje wiele korzyści dla uczniów klasy 7. Nie tylko pomaga w przygotowaniu do kartkówek i sprawdzianów, ale także rozwija kluczowe umiejętności, które mogą być przydatne
Zobacz także: