Ułamki dziesiętne możemy odejmować w pamięci lub sposobem pisemnym. Wybór odpowiedniej metody należy do nas. Zazwyczaj trudniejsze działania łatwiej rozwiązywać za pomocą odejmowania pisemnego.

Odejmując ułamki dziesiętne istotne są zasady, które poznaliśmy przy dodawaniu pisemnym ułamków dziesiętnych – osobno odejmujemy liczby całkowite, osobno części dziesiętne, setne itd. Odejmowanie zaczynamy od ostatnich cyfr. Jeżeli korzystamy ze sposobu pisemnego, nie możemy zapomnieć o odpowiednim umieszczeniu odpowiednich ułamków – całości w tych samych rzędach, przecinki w tych samych rzędach, części dziesiętne w tych samych rzędach itd. Gdy jeden ułamek ma mniej cyfry wystepujących po przecinku, wówczas w brakujące miejsca możemy wpisać zero.

Przykład I:

Oblicz: 3,6 – 1,2
Powyższy przykład możemy z łatwością wykonać w pamięci. 3,6 – 1,2 = 2,4

Przykład II:

Oblicz: 12,64 – 7,3
Podany przykład również możemy wykonać w pamięci. Drugi ułamek posiada jednak mniej cyfr po przecinku. W tym przypadku możemy dopisać do niego dodatkowe zero.

12,64 – 7,3 = 12,64 – 7,30 = 5,34

Przykład III:

Oblicz: 8,7642 – 4,263

Podany przykład jest znacznie trudniejszy niż pozostałe – najbezpieczniej i najłatwiej będzie obliczyć go sposobem pisemnym. Rozpoczynamy od prawidłowego zapisu działania – w osobnych rzędach całości, przecinki, części dziesiętne, setne, tysięczne itd. Dopisujemy również dodatkowe zero ułamkowi, który ma mniej cyfr po przecinku, tak aby ilość cyfr po przecinku podanych ułamków była równa.

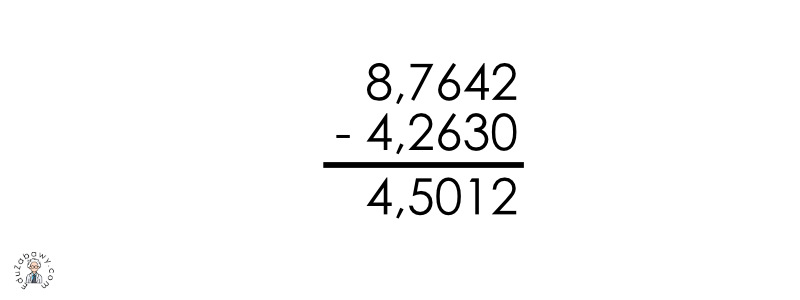
8,7642 – 4,263 = 4,5012

Przykład IV:

Oblicz: 6,02 – 3,123

Podany przykład również łatwiej obliczyć sposobem pisemnym. Nie zapomnij dopisać zera w odpowiednim miejscu.

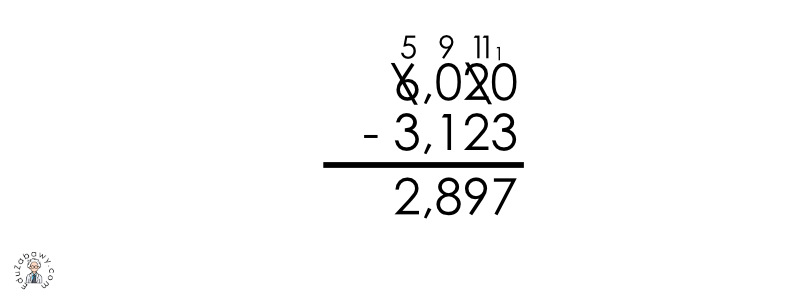
6,02 – 3,123 = 6,020 – 3,123 = 2,897

W powyższym przykładzie musieliśmy dokonać „pożyczenia” – jeżeli nie pamiętasz tej metody zachęcam Cię do zapoznania się z rozdziałem dotyczącym odejmowania pisemnego liczb całkowitych.

Zamiana ułamków dziesiętnych na ułamki zwykłe podczas odejmowania

Jeżeli łatwiej odejmuje nam się ułamki zwykłe, możemy zamienić ułamki dziesiętne na ułamki zwykłe i w ten sposób rozwiązać zadanie. Tak samo możemy zamienić ułamki zwykłe, jeżeli łatwiejsze dla nas jest odejmowanie ułamków dziesiętnych.

Zadania:

Oblicz:

1,5 – 1,1 = 1 5/10 – 1 1/10- = 4/10 = 0,4

3,65 – 0,21 = 3 65/100 – 21/100 = 3 44/100 = 3,44

81/100 – 17/100 = 0,81 – 0,17 = 0,64 = 64/100 = 16/25

Zastosowanie w praktyce, czyli ćwiczenia:

• Quizy na działania na ułamkach