Prostopadłościany i sześciany należą do figur przestrzennych, inaczej figur trójwymiarowych. Występują one w przestrzeni i możemy spotkać się z nimi w życiu codziennym. Przykładowymi prostopadłościanami są m. in. pralki, książki, kartony czy też pudełka.

Co powinieneś wiedzieć o prostopadłościanach?

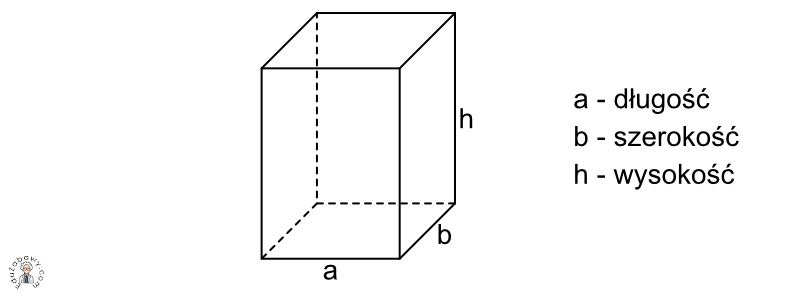
• Figury te oprócz podstawowych wymiarów takich jak długość i wysokość, posiadają jeszcze szerokość.
• Każdy prostopadłościan posiada 8 wierzchołków oraz 12 krawędzi.
• Każdy prostopadłościan posiada 6 ścian. Ściany te są prostokątami. Niektóre ściany są do siebie prostopadłe lub też równoległe.

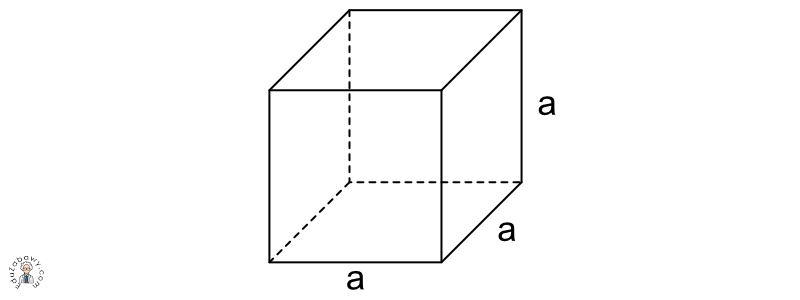
Ścianami sześcianów są z kolei kwadraty. W związku z tym wszystkie krawędzie tej figury są równe.

Przykład I:

Ścianami sześcianu są kwadraty, których krawędzie mają 5 cm. Oblicz długość wszystkich krawędzi sześcianu.

Wiemy, że każdy sześcian ma w sumie 12 krawędzi. Musimy więc pomnożyć długość jednej krawędzi razy ilość wszystkich krawędzi, aby otrzymać sumę wszyskich krawędzi.

12 • 5cm = 60cm

Długość wszystkich krawędzi sześcianu wynosi 60 cm.

Przykład 2:

Oblicz długości krawędzi prostopadłościanu o wymiarach 3 cm • 4 cm • 5 cm.

Podane zadanie jest już trochę bardziej wymagające. Musimy zastanowić się ile boków stanowiących wysokość, długość oraz szerokość ma prostopadłościan. Jeżeli spojrzymy na rysunki, które zostały przedstawione na początku omawiania tego tematu, zauważymy, że prostopadłościan ma cztery boki stanowiące jego długość, cztery boki stanowiące jego wysokość oraz cztery boki stanowiące jego szerokość. Aby więc uzyskać sumę długości jego krawędzi musimy każdą miarę pomnożyć razy cztery, a następnie otrzymane iloczyny dodać do siebie.

3 cm • 4 = 12 cm

4 cm • 4 = 16 cm

5 cm • 4 = 20 cm

12 cm + 16 cm + 20 cm = 48 cm

Suma długości krawędzi podanego prostopadłościanu wynosi 48 cm.

Przykład III:

Oblicz pole powierzchni prostopadłościanu o wymiarach 1 cm • 2 cm • 3 cm.

Aby obliczyć pole powierzchni prostopadłościanu, możemy skorzystać z następującego wzoru:

P = 2 • a • h + 2 • a • b + 2 • b • h = 2 • (a • b + a • h + b • h)

Wzór wydaje się skomplikowany, jednak bazuje on tylko i wyłącznie na obliczeniu pól poszczególnych prostokątów, a następnie dodaniu ich do siebie. Otrzymaną sumę mnożymy razy dwa, ponieważ każdy prostopadłościan składa się 6 ścian, które dzielą się na 3 pary (zawsze dwa takie same prostokąty).

a = 1 cm
b = 2cm
h = 3 cm

P=2•(1•2+1•3+2•3)cm²=2•(2+3+6)cm² =2•11 cm² = 22 cm²

Pole powierzchni prostopadłościanu wynosi 22 cm².

Zastosowanie w praktyce, czyli ćwiczenia i quizy:

• Quizy dla klasy 4
• Quizy dla klasy 5
• Quizy dla klasy 6
• Quizy dla klasy 7