Zanim przejdziemy do wyjaśniania czym są procenty, warto podkreślić, że każdy z Nas spotyka je w różnych sytuacjach. I nawet jeśli nie potrafisz ich obliczać, co za chwilę się zmieni, trafiłeś na procenty w telewizji, Internecie czy określeniu, że coś jest „pewne na 100%”.
Dlaczego 100%? Właśnie z tego względu, że oznacza to całość. W przypadku matematyki 100 procent jest liczbą całkowitą.
Lubisz zupę pomidorową albo słodkie ciasta z kremem? A kto nie lubi! Słyszałeś zapewne o śmietanie 18%, 30% lub nawet 36%.
Choć udziału w wyborach prezydenckich, parlamentarnych nie możesz jeszcze brać, spotkałeś się z terminem sondaż wyborczy. Jest to przedstawienie w procentach właśnie ilości uzyskanych głosów.
Dobrze, skupmy się teraz na procentach z matematycznego punktu widzenia. Najprostszym przykładem jest przedstawienie czym tak właściwie jest 1%. Spójrzmy poniżej:
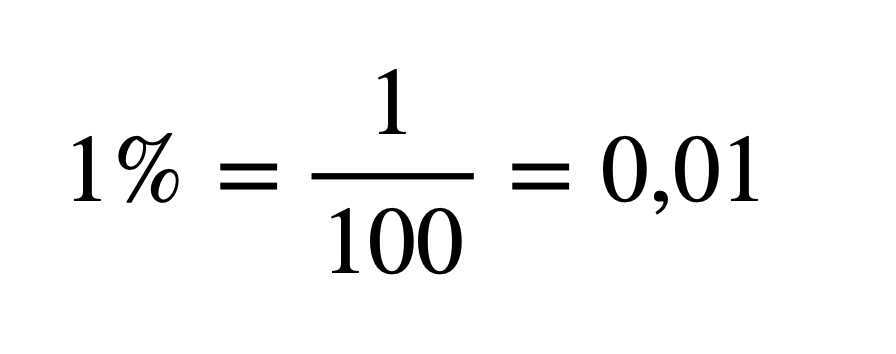
Jak widać procenty można z łatwością przedstawiać jako ułamek, zarówno zwykły jak i dziesiętny. Taka możliwość zamiany znacznie ułatwi Nam rozwiązywanie równań matematycznych, o czym przekonasz się w kolejnych tematach.
Procenty jest łatwo wyrazić, gdy dotyczą liczby sto. Zobaczmy na przykładach:
Jeśli uczeń chce otrzymać wyróżnienie czytelnicze, musi w ciągu roku szkolnego wypożyczyć 100 książek.
W marcu Asia miała wypożyczonych 69 książek, Marek 40 a Krysia 80. Obliczmy teraz procent poszczególnych osób.
Asia na 100 książek do wypożyczenia, miała zapisane 69, mówimy więc, że wypożyczyła 69% książek.
W przypadku Marka mamy 40 na 100, a więc powiemy, że wypożyczył on 40% książek.
Krysia natomiast, ma na karcie bibliotecznej 80 książek na 100. Powiemy, że wypożyczyła aż 80% książek.
Takie przedstawienie procentów jest banalnie proste, prawda?! Mamy tu do czynienia z pełnymi setkami, dlatego nie pojawiły się żadne problemy. Jak jednak należy postępować w sytuacji, gdy chcemy obliczyć, ile procent uczniów w klasie 6 bierze udział w konkursie czytelniczym.
W klasie 6 jest 25 uczniów. 17 z nich wypożycza książki w ramach akcji czytelniczej. Jaki to procent? Zapiszmy dane:
25 uczniów jest w klasie
17 z nich wypożycza książki
Zapisujemy ułamek 17 25 , wiemy jednak już, że ułamek ten możemy sobie rozszerzyć tak by w mianowniku pojawiła się liczba 100. Zatem postępujemy jak w przykładzie 17 25 = 14x4 25x4 = 68 100 , możemy więc powiedzieć, że 68 % uczniów w klasie 6 bierze udział w akcji czytelniczej.
Zawsze, gdy chcemy daną liczbę zapisać w postaci procentów, należy sprowadzić ją do pełnej 100, jak wykonaliśmy to w przykładzie powyżej.


0 Komentarzy