Liczbę wymierną stanowi każda liczba, którą możemy przedstawić w postaci ułamka zwykłego p q , gdzie p jest jakąkolwiek liczbą całkowitą, a q jest liczbą całkowitą różną od zera.
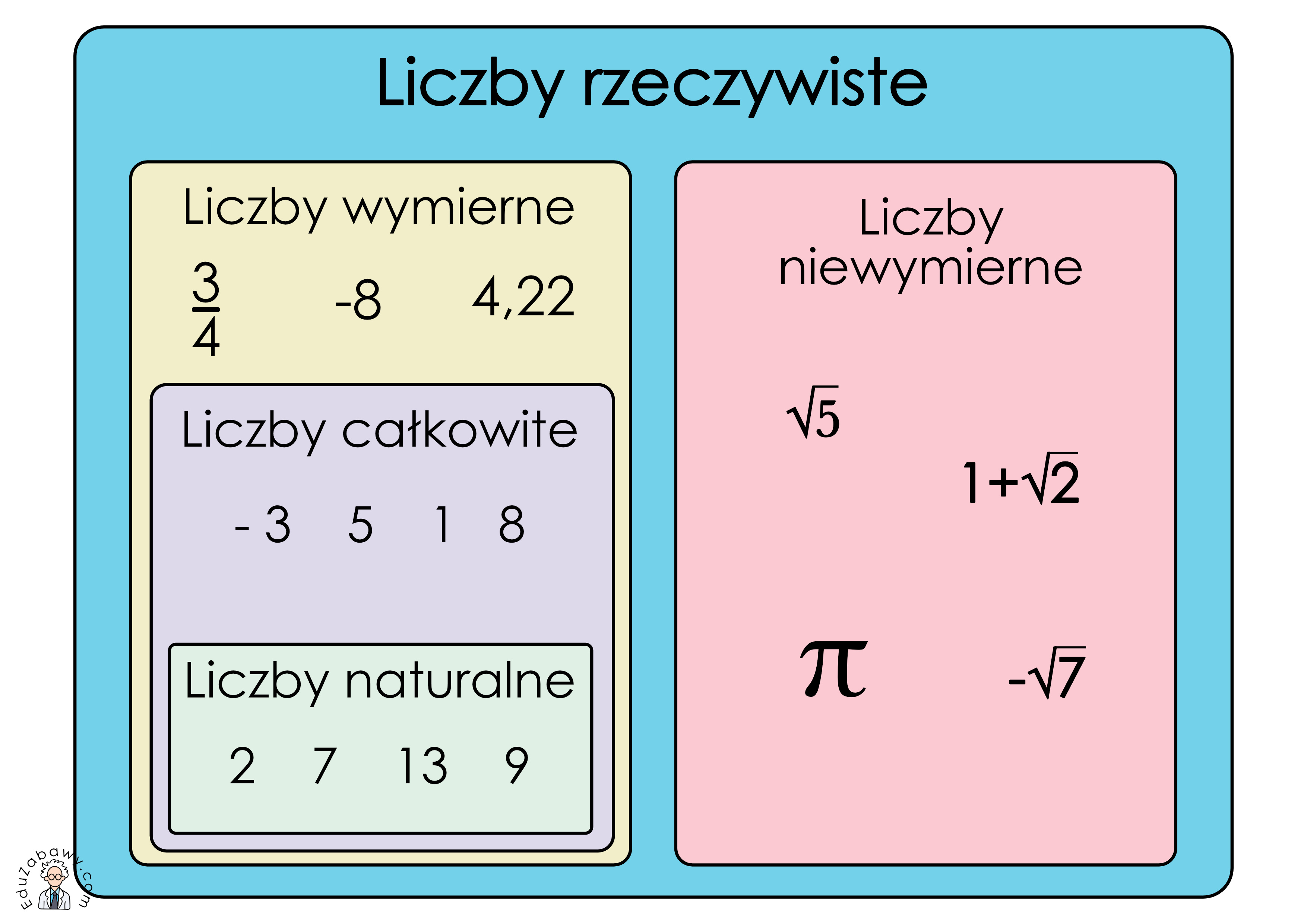
Podsumowując: do zbioru liczb wymiernych zaliczamy liczby całkowite oraz ułamki.
Jak prawidłowo opisać zbiór liczb wymiernych?
Zbiór liczb wymiernych przedstawiamy za pomocą litery Q, np. Q = {1⁄2, 3⁄4, 5, 7}.
Przykład I:
Które liczby należą do zbioru liczb wymiernych?
1; 1,5; 3 4 ; √7; 0,(1); – 6 7 ; -5, liczba Pi
Q = {1; 1,5; 3 4 ; 0,(1); – 6 7 ; -5}
Liczb wymiernych nie stanowią pierwiastki, których nie jesteśmy w stanie przedstawić za pomocą ilorazu liczb całkowitych.
Uwaga! Zero jest liczbą wymierną, ponieważ jesteśmy w stanie przedstawić je za pomocą ułamka np. 0 3 .
Więcej o liczbach:



0 komentarzy