Ułamki dziesiętne możemy dodawać zarówno w pamięci, jak i pisemnie – wszystko zależy od stopnia skomplikowania działania. Główną zasada, o której należy zawsze pamiętać wskazuje na to, że należy do siebie dodawać odpowiednio każdą część ułamka – części całkowite, części dziesiętne, części setne itd.

Przykład I:

Wykonaj dodawanie: 1,2 + 2,4

1,2 + 2,4 = 3,6

Zawsze musimy pamiętać o dodaniu do siebie odpowiadających sobie nawzajem części – dodajemy do siebie całości (1 + 2 = 3) oraz części dziesiętne (2 + 4 = 6).

Przykład II:

Wykonaj dodawanie: 3,7 + 1,4

3,7 + 1,4 = 5,1

Przy dodawaniu części dziesiętnych otrzymaliśmy liczbę 11 – jest ona większa od 9. W takiej sytuacji należy przenieść jedną całość przed przecinek, czyli dodać do liczby całkowitej. Całość to inaczej 10 – po jej przeniesieniu zostaje nam liczba jeden, która stanowi część dziesiętną sumy ułamków.

W podanych przykładach dodawane ułamki mają tyle samo cyfr po przecinku. Jak należy jednak postąpić, gdy ułamki mają różną ilość cyfr po przecinku?
W takim przypadku wystarczy dopisać zera liczbie, która ma mniej cyfr po przecinku tak, aby dane liczby miały tyle samo cyfr po przecinku.

Przykład III:

Wykonaj dodawanie: 4,36 + 3,2

4,36 + 3,2 = 4,36 + 3,20 = 7,56

Przykład IV:

Wykonaj dodawanie: 8,2976 + 4,12

8,2976 + 4,12 = 8,2976 + 4,1200 = 12,4176

Dodawanie ułamków dziesiętnych sposobem pisemnym

Jeżeli nie jesteśmy w stanie dodać do siebie ułamków dziesiętnych w pamięci, możemy skorzystać z dodawania pisemnego. Obowiązują tutaj bardzo zbliżone zasady do tych, które stosowaliśmy przy dodawaniu sposobem pisemnym liczb całkowitych – zaczynamy dodawać poszczególne cyfry od końca. Musimy jednak pamiętać, aby zapisać poszczególne cyfry grup pod sobą, czyli w jednym rzędzie – przecinki poszczególnych ułamków muszą znajdować się pod sobą. Dzięki temu utworzymy osobne rzędy dla liczb całkowitych, części dziesiętnych, setnych itd. Jeżeli liczby nie mają tej samej liczby cyfr występujących po przecinku, to wówczas w brakujące miejsca wpisujemy zera.

Przykład I:

Wykonaj dodawanie: 8,12 + 4,7625

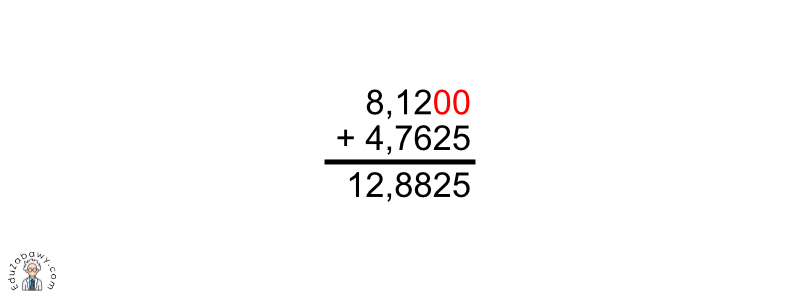
Po odpowiednim wykonaniu dodawania musimy pamiętać, aby umieścić przecinek w rzędzie, w którym umieściliśmy przecinki dodawanych do siebie ułamków

Przykład II:

Wykonaj dodawanie: 3,762 + 8,227

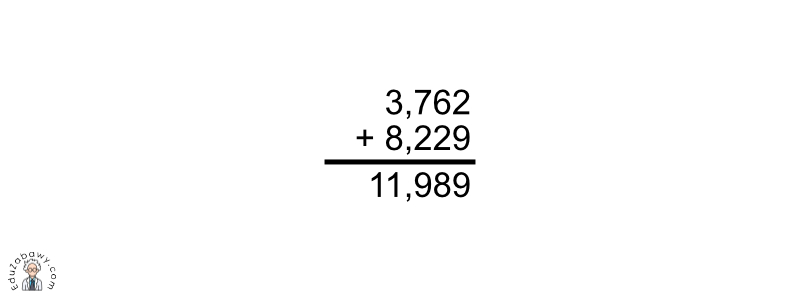
Dodawanie przy pomocy zamiany ułamków dziesiętnych na ułamki zwykłe

Możliwa jest zamiana ułamków dziesiętnych na ułamki zwykłe (lub odwrotnie) w trakcie dodawania. Warto z niej skorzystać, jeżeli dzięki temu łatwiej nam będzie rozwiązać dany przykład.

Przykład I:

Wykonaj dodawanie: 0,3 + 0,5

0,3 + 0,5 = ³ ₃₀ + ⁵ ₁₀ = ⁸ ₁₀ = 0,8

Przykład II:

Wykonaj dodawanie: ⁷ ₁₀ + ¹ ₁₀

⁷ ₁₀ + ¹ ₁₀ = 0,7 + 0,1 = 0,8

Zastosowanie w praktyce, czyli ćwiczenia:

• Ułamki dziesiętne
• Ułamki zywkłe
• Liczby naturalnie ułamki