Równania matematyczne to takie działania, w których występuje przynajmniej jedna niewiadoma. Z kolei niewiadoma to liczba, która kryje się za daną literą. Aby odkryć jej tożsamość i wyprowadzić jej wartość, musimy rozwiązać dane równanie matematyczne.
Poniżej przedstawione zostały równania matematyczne z jedną niewiadomą.
6 - y = 4; gdzie y stanowi niewiadomą, a całe działanie określamy mianem równania matematycznego
5 + g = 62; gdzie g stanowi niewiadomą, a całe działanie określamy mianem równania matematycznego
Teraz spróbujmy rozwiązać powyższe równania: 6 -y = 4
Oczywiście wiemy, że y to 2, ponieważ 6 - 2 da nam 4
5 + g = 62
Tutaj również łatwo możemy odgadnąć, że g to 57, ponieważ 5 + 57 da nam 62
Przy rozwiązywaniu tych równań skorzystaliśmy z właściwości dodawania i odejmowania, która stanowi, że dodawanie i odejmowanie to działania odwrotne. Idealnie obrazuje to następujący diagram:
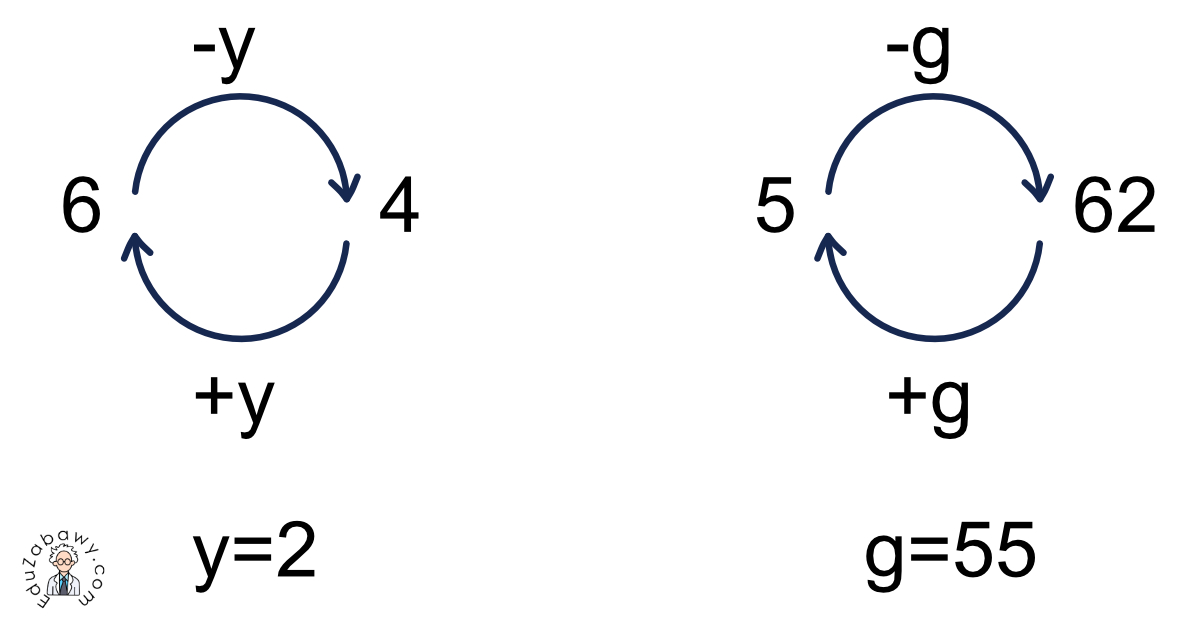
Poniżej przedstawione zostały w sposób matematyczny rozwiązania powyższych równań:
6 -y = 4
6 -4 = y
y= 2
5 + g = 62
g = 62 - 5
g = 57
W trakcie rozwiązywania równań matematycznych możemy spotkać się z takimi określeniami jak lewa strona równania lub też prawa strona równania. Lewą stronę równania stanowi wszystko to, co znajduje się po przed znakiem równości, a prawą wszystko to, co znajduje się za znakiem równości. W matematyce dążymy do tego, aby po lewej i prawej stronie znajdowały się takie same liczby.
Przykład I: Rozwiąż następujące równanie: 4x + 4 = 28
Na początku przenosimy liczbę 4 na drugą stronę równania tak, aby niewiadoma została po jednej stronie:
4x = 28 - 4
4x = 24
Następnie dzielimy obie strony równania przez 4 tak, aby po jednej stronie została sama niewiadoma:
4x = 24 /:4
x= 6
Przykład II: Rozwiąż następujące równanie: 4x + 32 = 2x + 48
Na początek porządkujemy równanie tak, aby po jednej stronie znajdowały się niewiadome:
4x - 2x = 48 - 32
2x = 16
Następnie dzielimy obie strony równania przez 2:
2x = 16 /:2
x= 8


0 Komentarzy