Największy wspólny dzielnik to największa liczba, która pozwala nam podzielić dwie liczby całkowite w taki sposób, że dzielenie nie będzie miało reszty.
Największy wspólny dzielnik zapisuje się w skrócie jako NWD.
Przykład I:
Jaki jest NWD liczb 8 i 12?
Aby znaleźć najwyższy dzielnik, który podzieli nam zarówno liczbę 8, jak również 12 bez reszty możemy wypisać wszystkie dzielniki tych liczb, a następnie wybrać ten, który jest dla nich wspólny i najwyższy.
Dzielniki liczby 8 = 1; 2; 4; 8
Dzielniki liczby 12 = 1; 2; 3; 4; 6; 12
Łatwo zauważyć, że podane liczby mają kilka wspólnych dzielników, a ich najwyższy wspólny dzielnik wynosi 8.
Odnalezienie NWD na tym poziomie wydaje się bardzo proste. Co możemy jednak zrobić, gdy mamy za zadanie odnaleźć NWD dla większych liczb, np. dla 48 i 36? Możemy wypisywać wszystkie dzielniki dla każdej z liczb osobno. Rozwiązanie takie pociąga jednak za sobą ryzyko popełnienia błędu. Poniżej przedstawiony został sposób znalezienia NWD przy pomocy rozkładu liczb na czynniki pierwsze - jest on znacznie łatwiejszy i mniej czasochłonny.
Przykład II:
Znajdź NWD dla liczb 48 i 36.
Aby odnaleźć NWD dla podanych liczb rozkładamy je równocześnie na czynniki pierwsze. Po lewej stronie kreski zapisujemy liczby, które rozkładamy, a po prawej stronie ich dzielniki. Pierwszym najmniejszym wspólnym dzielnikiem liczb jest liczba 2. Zapisujemy ją w odpowiednim miejscu (czyli po prawej stronie kreski). Dokonujemy rozkładu liczb na czynniki pierwsze aż do chwili, w której niemożliwe będzie znalezienie wspólnego dzielnika.
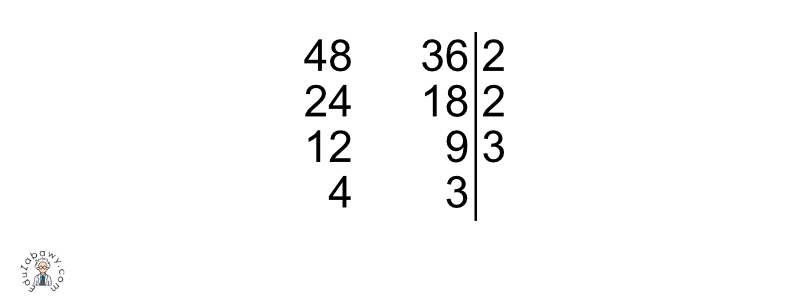
NWD tworzy iloraz dzielników znajdujących się po prawej stronie kreski - w podanym przykładzie będzie to iloraz liczb 2; 2 oraz 3.
2 x 2 x 3 = 12
Największym wspólnym dzielnikiem dla liczb 48 oraz 36 jest 12.
Przykład VI:
Znajdź NWD dla liczb 27 i 36
Dokonujemy wspólnego podziału liczb na czynniki pierwsze.
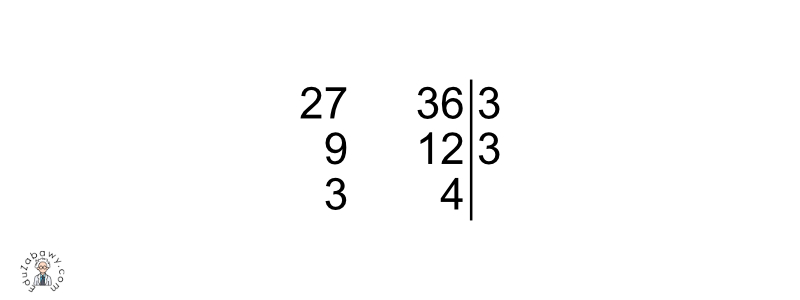
Następnie mnożymy wszystkie liczby znajdujące się po prawej stronie kreski.
3 x 3= 9
Największym wspólnym dzielnikiem dla liczb 27 i 36 jest 9.
Przy ustalaniu NWD niezwykle pomocne są cechy podzielności liczb oraz rozkład liczb na czynniki pierwsze. Pamiętaj o regularnym utrwalaniu przerobionego materiału, aby łatwo przyswajać nowe zagadnienia.


0 Komentarzy