Najmniejszą wspólną wielokrotność wyznacza się dla dwóch lub też większej ilości liczb. Stanowi ona liczbę, która jest zarówno wielokrotnością danych liczb, jak również jest najmniejszą spośród wszystkich możliwych dla danych liczb wielokrotności.
Najmniejszą wspólną wielokrotność zapisuje się w skrócie jako NWW.
NWW musi być większa od zera.
Przykład I:
Wyznacz NWW dla liczb 4 i 7.
NWW możemy wyznaczyć przez poprawne wypisanie wielokrotności podanych liczb:
W4 = 4, 8, 12, 16, 20, 24, 28, 32, 36 …
W7 = 7, 14, 21, 28, 35, 42 …
Powyższe rozpisanie pozwala nam zauważyć, że pierwszą (czyli najmniejszą) wspólną wielokrotnością dla liczb 4 i 7 jest 28.
NWW (4; 7) = 28
Jak jednak powinniśmy postąpić, gdy musimy wyznaczyć NWW większych liczb, np. 24 i 36? Odpowiednie wypisywanie poszczególnych wielokrotności może nam sprawić wiele trudności oraz pochłonąć dużo czasu. Na szczęście istnieją dwa sposoby, które ułatwią nam to zadanie.
Sposób I – Określenie NWW przy pomocy rozkładu liczb na czynniki pierwsze.
Przykład I:
Wyznacz NWW liczb 24 i 36.
Pierwszą rzeczą, którą musimy zrobić jest rozłożenie podanych liczb na czynniki pierwsze.
24 = 2 x 2 x 2 x 3
36 = 2 x 2 x 3 x 3
Następnie z drugiej rozłożonej liczby wykreślamy te czynniki pierwsze, które pojawiły się również w pierwszej rozłożonej liczbie.
24 = 2 x 2 x 2 x 3
36 = 2 x 2 x 3 x 3
Pozostałe, nieskreślone liczby mnożymy:
2 x 2 x 2 x 3 x 3 = 72
Otrzymany iloczyn to NWW podanych liczb.
NWW (24, 36) = 72
Przykład II:
Wyznacz NWW liczb 25 i 9. Rozbijamy podane liczby na czynniki pierwsze:
25 = 5 x 5 9 = 3x 3
W tym przypadku żadne liczby się nie powtarzają – mnożymy je więc wszystkie.
NWW = 5 x 5 x 3 x 3 = 225
NWW (15; 9) = 225
Sposób II – Określenie NWW przy pomocy największego wspólnego dzielnika
Przykład I:
Wyznacz NWW liczb 24 i 36.
Najpierw wyznaczamy NWD liczb 24 i 36.
NWD (24, 36) = 12
Największa wspólna wielokrotność danych liczb to inaczej iloraz tych liczb dzielony przez ich NWD.
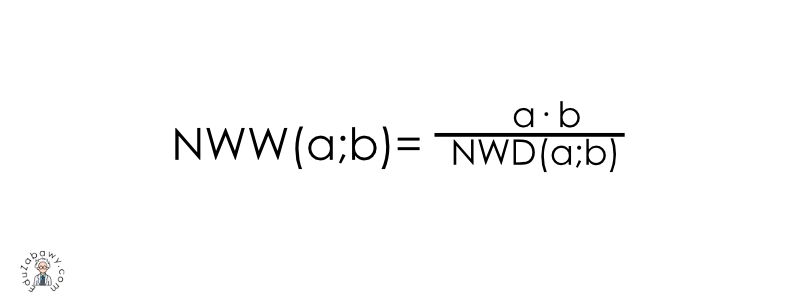
Obliczamy NWW według podanego wzoru.
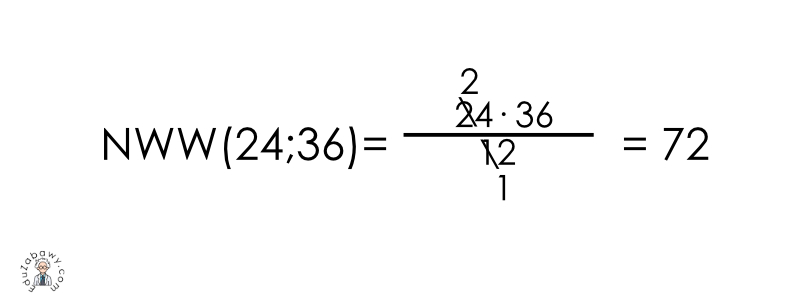
Otrzymany wynik stanowi szukaną największą wspólną wielokrotność dla liczb 24 i 36.
NWW (24, 36) = 72
Wyznaczanie NWW jest szczególnie przydatne w trakcie szukania wspólnego mianownika różnych ułamków.



0 komentarzy