Jedną z cech liczb złożonych jest to, że można je przedstawić za pomocą iloczynu samych liczb prostych.
Przykład I:
12 = 2 x 2 x 3
16 = 2 x 2 x 2 x 2
Jak jednak znaleźć odpowiednie mnożne i mnożniki będące liczbami pierwszymi, których iloczyn da nam liczbę złożoną? O ile w przypadku liczby 8, czy 12 łatwo je odnaleźć, o tyle w przypadku liczby 146, czy 82 może to już być trochę bardziej skomplikowane. Poniżej przedstawiony został sposób, który pozwoli nam szybko i bez problemów znaleźć prawidłowe liczby. W matematyce sposób ten określa się rozkładem liczby na czynniki pierwsze.
Przykład II:
Rozłóż liczbę 36 na czynniki pierwsze.
Rozkład liczby na czynniki pierwsze rozpoczynamy od odpowiedniego zapisu – po lewej stronie kartki zapisujemy liczbę, którą chcemy rozłożyć, a po jej prawej stronie rysujemy pionową kreskę.
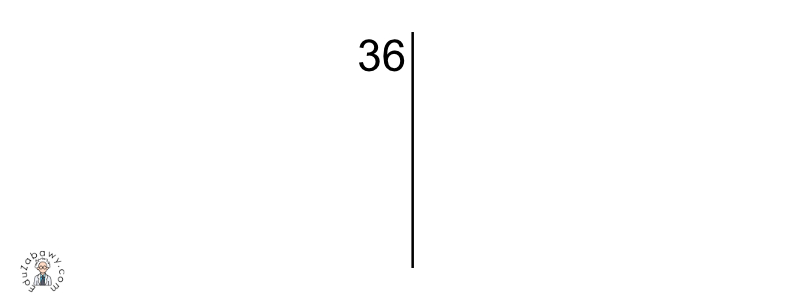
Następnie dzielimy tą liczbę, którą zapisaliśmy po lewej stronie kreski (36) przez najmniejszą możliwą liczbę pierwszą tak, aby otrzymany wynik nie posiadał reszty. W tym przypadku taką liczbą będzie 2. Po prawej stronie kreski, na tej samej wysokości na której znajduje się liczba 36 zapisujemy nasz dzielnik, czyli 2. Wynik dzielenia, czyli 18 zapisujemy po lewej stronie, pod liczbą, która stanowiła dzielną, czyli pod 36.
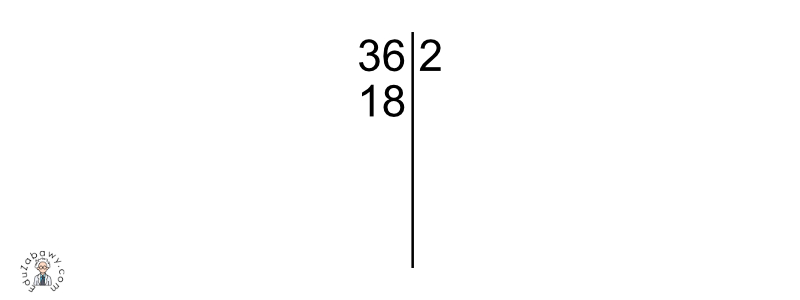
Teraz poszukujemy kolejnej liczby pierwszej, która pozwoli nam podzielić liczbę 18 bez reszty. W tym przypadku również odpowiednia będzie liczba 2. Dokonujemy dzielenia.
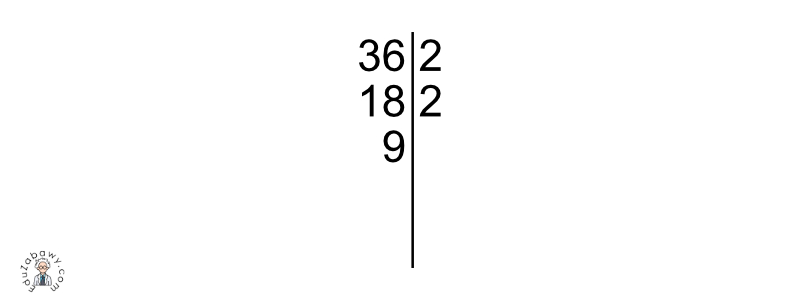
Powyższe czynności powtarzamy tak długo, aż po lewej stronie kreski pojawi się liczba 1 – będzie to wówczas oznaczać, że liczba została całkowicie rozłożona na czynniki pierwsze.
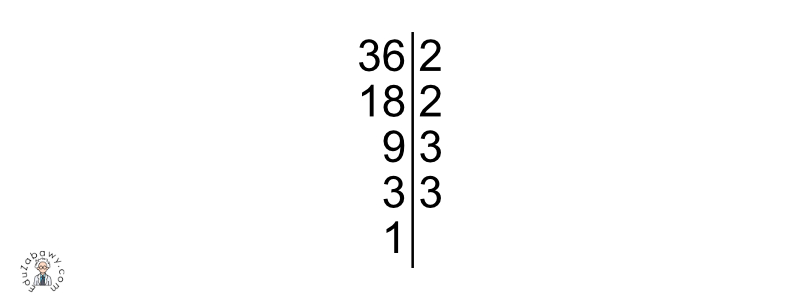
Liczby, które widnieją po prawej stronie kreski to czynniki pierwsze – ich iloczyn jest równy liczbie, którą rozkładaliśmy na czynniki pierwsze.
36 = 2 x 2 x 3 x 3
Ważne: Po prawej stronie kreski mogą znajdować się jedynie liczby pierwsze – tylko one stanowią czynniki pierwsze.



0 komentarzy