Wyobraź sobie sytuację, że od poniedziałku do piątku dostajesz od rodziców po 10 zł, które wkładasz do skarbonki. W weekend otrzymujesz od rodziców jednorazowo 50 zł. Jakie oszczędności zgromadzisz w skarbonce po tygodniu? 

Pieniądze, które znajdują się w skarbonce możesz zapisać matematycznie jako:

5⋅10+50=50+50=100

Po tygodniu zaoszczędzisz więc 100 zł.

Zastanów się, czy gdyby rodzice wrzucili Ci do skarbonki 50 zł w poniedziałek, a następnie od wtorku do soboty dawali codziennie po 10 zł, czy po tygodniu nadal w śwince skarbonce miałabyś 100 zł?

Jeśli na powyższe pytanie odpowiedziałeś TAK, masz rację. 

Popatrz jednak na na zapis matematyczny drugiej sytuacji:

50+5⋅10=…

Wykonując to działanie od lewej do prawej wynik prezentowałby się tak:

50+5⋅10=55⋅10=550

Wiesz jednak, że ten wynik nie jest prawidłowy – w skarbonce znajduje się przecież 100 zł! Z pomocą przychodzi kolejność wykonywania działań. Dzięki jednolitym zasadom wyniki działań nie różnią się pomimo różnicy zapisu. 

Zapamiętaj w jakiej kolejności wykonujemy działania matematyczne: 

• 1. Działania w nawiasach zawsze wykonujemy pierwsze. 
• 2. Po obliczeniu tego, co w nawiasach, wykonujemy potęgowanie i pierwiastkowanie
• 3. Potem obliczamy mnożenie i dzielenie.
• 4. Ostatnie w kolejności wykonujemy dodawanie i odejmowanie.

Spójrz na przykładowe działania i ich rozwiązania:

Działania, w których znajdują się jedynie dodawanie i odejmowanie, liczymy od lewej do prawej strony, np.:

12−6+3=6+3=9

Działania, w których występuje tylko mnożenie i dzielenie, liczymy też od lewej do prawej, np.:

24:8⋅4=3⋅4=12

Jeżeli w działaniu matematycznym występuje potęgowanie, zaczynamy właśnie od niego, np.:

32:2²=32:4=8

3⋅5²=3⋅25=75

Jeżeli w zadaniu występują różne działania, na początku liczymy potęgi, kolejnie mnożenie i dzielenie (od lewej do prawej), a ostatnie dodawanie i odejmowanie (także od lewej do prawej), np.:

15+5⋅2=15+10=25

Jeżeli w działaniu występują działania w nawiasach, najpierw liczymy to, co znajduje się w środku nawiasów, a potem wykorzystujemy poznanezasady dotyczące kolejności wykonywania działań, np.:

9⋅(5+2)=9⋅7=63

Zadania kontrolne:

Zadanie 1. Oblicz: 

5⋅(7−8:4)

Zadanie 2. 

Bez wykonywania obliczeń oceń, czy  112+(15⋅14−6) jest równe (15⋅14−6)+112

Przygotowaliśmy też plansze dydaktyczne: Kolejność wykonywania działań w pliku PDF i gotowe do druku (bez znaku wodnego) za darmo. Podgląd jednej z plansz:

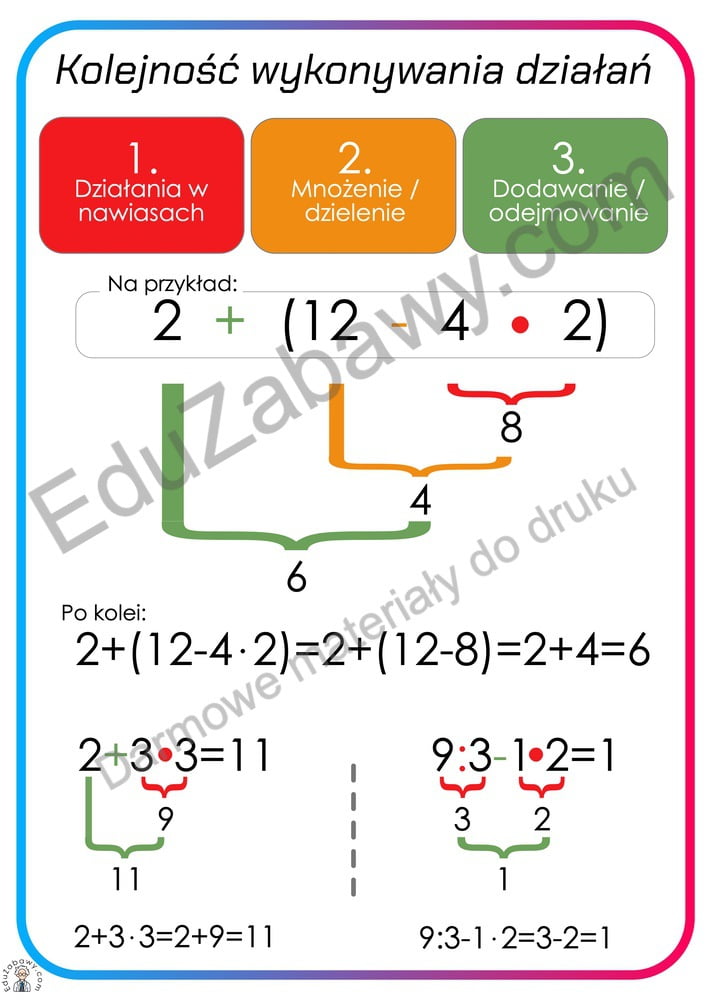
Zastosowanie w praktyce, czyli ćwiczenia:

• Quiz: Kolejność wykonywania działań z nawiasami – mnożenie i dodawanie
• Quiz: Kolejność wykonywania działań bez nawiasów – dzielenie i odejmowanie
• Quiz: Kolejność wykonywania działań bez nawiasów – mnożenie i dodawanie
• Quiz: Kolejność wykonywania działań z nawiasami – dzielenie i odejmowanie
• Quiz: Kolejność wykonywania działań – zadania tekstowe