Aby obliczyć pole trójkąta, musimy pomnożyć jego podstawę oraz wysokość opuszczoną na tą podstawę, a następnie otrzymany iloczyn podzielić przez 2.
Wzór na pole trójkąta:
P = a x h x 1 2
Zasada ta sprawdza się dla trójkąta równobocznego, prostokątnego, równoramiennego, rozwartokątnego, różnobocznego, ABC.
Przykład I:
Oblicz pole powierzchni trójkąta, którego bok ma 4 cm, a wysokość opuszczona na ten bok ma 3 cm.
a = 4 cm
h = 3 cm
P = 4 cm x 3 cm x 1 2 = 12 cm2 x 1 2 = 6 cm2
Pole trójkąta wynosi 6 cm2.
Przykład II:
Oblicz pole poniższego trójkąta:
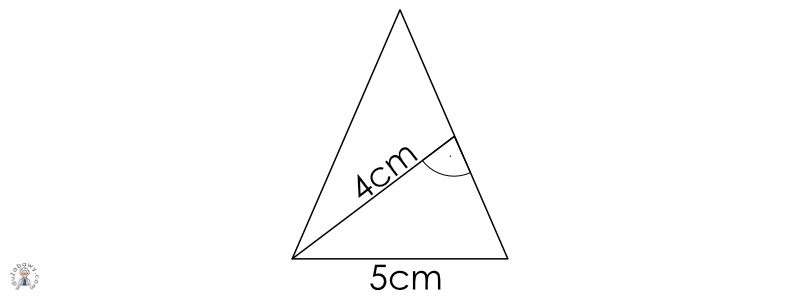
Obliczając powierzchnię trójkąta, musimy pamiętać, aby pomnożyć bok oraz wysokość właściwą dla danego boku. Na rysunku mamy przedstawioną niewystarczającą ilość danych - nie ma podanej wysokości odpowiedniej dla opisanego boku. W związku z tym nie możemy obliczyć pola powierzchni trójkąta.
Przykład III:
Oblicz pole poniższego trójkąta:
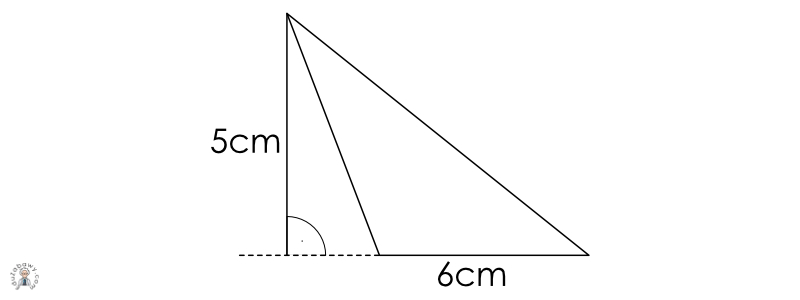
a= 6
h= 5
p = 6 x 5 x 1 2 = 30 x 1 2 = 15
Pole powierzchni podanego trójkąta wynosi 15 jednostek kwadratowych.
Przykład IV:
Pole powierzchni trójkąta wynosi 12 cm2. Długość podstawy trójkąta to 6 cm. Jaką długość ma wysokość, która opada na podany bok?
W podanym zadaniu mamy podane następujące dane:
P = 12 cm²
a = 6 cm
h= ?
Wiemy również, że wzór na pole trójkąta wygląda następująco:
P = a x h x 1 2
Podstawiamy wszystkie zebrane dane do wzoru:
12 cm² = 6 x h x 1 2 = 6 x 1 2 x h
Mnożymy 6 i 1 2 :
12 cm² = 6 x 1 2 x h = 1 2 x h = 3 x h
12cm2 = 3 x h
Zastanawiamy się teraz ile razy musimy pomnożyć 3, aby otrzymać 12.
3 x 4 = 12
Wysokość trójkąta wynosi 4 cm.


0 Komentarzy