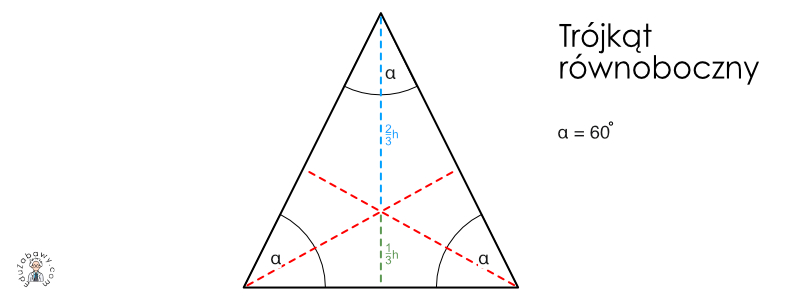
Mianem trójkąta równobocznego określamy trójkąt, którego wszystkie boki są równe, a każdy z jego kątów ma 60 stopni.

Pole trójkąta równobocznego – wzór

Obliczając pole trójkąta równobocznego możemy skorzystać z podstawowego wzoru na pole trójkąta – a x h/2. Istnieje jednak jeszcze jeden wzór, który jest dedykowany tylko i wyłącznie trójkątom równobocznym, a przedstawia on się następująco:

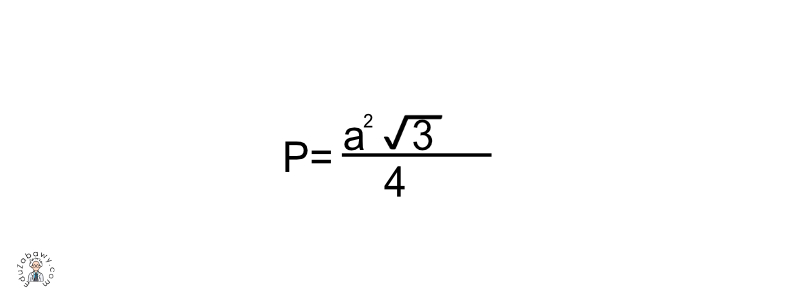
Możemy również obliczyć długość wysokości trójkąta za pomocą specjalnego wzoru na wysokość trójkąta równobocznego. ^{H = a√3} ₂

Co musisz wiedzieć o trójkątach równobocznych?

• Wysokość trójkąta jest równocześnie symetralną trójkąta. Jeżeli ją poprowadzimy, to otrzymamy dwa jednakowe trójkąty prostokątne, których kąty mają odpowiednio 90, 60 oraz 30 stopni.
• Wysokości trójkątów spotykają się w charakterystycznym punkcie. Punkt przecięcia się wysokości dzieli każdą wysokość na dwa odcinki. Odcinek poprowadzony od wierzchołka, aż do punktu spotkania się wysokości ma długość ² ₃ wysokości ( ² ₃ h). Z kolei odcinek poprowadzony od boku trójkąta, aż do punktu przecięcia się wysokości ma długość ¹ ₃ wysokości ( ¹ ₃ h).
• Miejsce, w którym przecinają się wszystkie wysokości trójkąta, stanowi równocześnie środek okręgu opisanego i wpisanego w trójkąt.
• Promień okręgu wpisanego w trójkąt stanowi ¹ ₃ jego wysokości. Jego długość możemy więc wyliczyć na podstawie następującego wzoru: r = ¹ ₃ h.
• Promień okręgu opisanego na trójkącie stanowi ² ₃ jego wysokości. Jego długość możemy więc wyliczyć na podstawie następującego wzoru: R = ² ₃ h = ^a√3 ₃ .

Zastosowanie w praktyce, czyli ćwiczenia i quizy:

• Figury geometryczne (klasa 4)
• Figury i kąty (klasa 5)
• Figury na płaszczyźnie (klasa 6)
• Geometria przestrzenna (klasa 6)